На покоящуюся на гладкой горизонтальной поверхности систему, состоящую из двух шариков массой $m$ каждый, соединенных пружиной, налетает слева шарик массой $M$ (рис.). При этом происходит лобовой абсолютно упругий удар. Найти приближенно отношение масс $\frac{m}{M} = \gamma$, при котором удар произойдет еще раз.
 Подробнее
Подробнее
На невесомой нити длиной $l$ привязан тяжелый шарик массой $m$; сила трения шарика о воздух пропорциональна скорости его движения относительно воздуха: $F_{тр}=\mu v$. Дует горизонтальный сильный ветер с постоянной скоростью $v$.
Определите период $T$ малых колебаний. Считать, что колебания шарика затухают за время, мною большее периода колебаний.
Подробнее
Тонкий абсолютно жесткий невесомый стержень, на конце которого закреплен точечный шарик, отклонили на небольшой угол $\alpha$ от положения равновесия и отпустили. В момент, когда стержень составлял угол $\beta < \alpha$ с вертикалью, произошло абсолютно упругое соударение шарика с наклонной стенкой (рис.).
Определите отношение $T_{1}/T$ периода колебаний такого маятника к периоду математического маятника той же длины.
 Подробнее
Подробнее
На чашку пружинных весов массой $M$ с некоторой высоты падает шарик массой $m$ $(M \gg m)$. Жесткость пружины равна $k$.
Определите смешение $\Delta x$ точки, около которой будет совершать колебания стрелка весов. Считать удары шарика о чашку абсолютно упругими.
Подробнее
По длинной проволоке, изогнутой в вертикальной плоскости в виде графика некоторой функции, может двигаться без трения бусинка массой $m$. Пусть $l_{A}$ - длина участка проволоки от начала координат до некоторой точки А. Известно, что если отпустить бусинку в точке А, такой, что $l_{A} < l_{A_{0}}$, то ее движение будет строго гармоническим: $l(t) = l_{A} \cos \omega t$.
Докажите, что существует такая точка В ($l_{A_{0}} \leq l_{B}$). в которой условие гармоничности колебаний будет нарушено.
Подробнее
На горизонтальной плоскости лежат два бруска массами $m$ и $2m$, соединенные пружиной жесткости $k$.
Найдите период $T$ малых продольных колебаний системы. Трением пренебречь.
Подробнее
Тяжелое круглое бревно подвесили за концы на двух канатах так, что расстояние между точками подвеса каждой веревки равно диаметру бревна. Длина каждого вертикального участка канатов равна $l$.
Определите период $T$ малых колебаний системы в вертикальной плоскости, перпендикулярной бревну.
Подробнее
На горизонтальных рельсах находится груз массой $M$. К нему прикреплен маятник - шарик массой $m$ на невесомой нерастяжимой нити. Груз может двигаться только вдоль рельсов.
Найдите отношение периодов $T_{2}/T_{1}$ малых колебаний маятника в параллельной и перпендикулярной рельсам вертикальных плоскостях.
Подробнее
Четыре невесомых стержня длины $l$ каждый соединены шарнирно и образуют ромб (рис.). Шарнир А закреплен, а к шарниру С подвешен груз. Шарниры D и В соединены невесомой пружиной, имеющей в недеформированном состоянии длину $1,5 l$. В положении равновесия стержни образуют с вертикалью углы $\alpha_{0} = 30^{\circ}$.
Найдите период $T$ малых колебаний груза.
 Подробнее
Подробнее
Тонкий обруч, шарнирно закрепленный в точке А, располагают в начальный момент так, что его центр масс находится почти прямо над точкой А (рис. 1). После этого обруч отпускают без толчка, и спустя время $\tau = 0,5$ с центр масс обруча занимает крайнее нижнее положение.
Определите время $t$, за которое вернется в нижнее положение равновесия маятник, представляющий собой массивный шарик В, закрепленный на невесомом жестком стержне, длина которого равна радиусу обруча, если в начальный момент шарик занимал почти крайнее верхнее положение (рис. 2) и был отпущен без толчка.

рис.1

рис.2
Подробнее
Невесомый жесткий стержень с грузом на конце прикреплен шарнирно в точке А к стене так, что может поворачиваться во все стороны (рис.). Стержень удерживается в горизонтальном положении вертикальной нерастяжимой нитью длины $l$, прикрепленной к его середине. Грузу сообщили импульс, перпендикулярный плоскости рисунка.
Найдите период $T$ малых колебаний системы.
 Подробнее
Подробнее
Одна веревка качелей закреплена выше другой личину $h$. Расстояние между столбами качелей равно $a$. веревок равны $l_{1}$ и $l_{2}$, причем $l^{2}_{1}+l^{2}_{2}=a^{2}+b^{2}$ (рис.).
Найдите период $T$ малых качаний на таких качелях. Размерами человека пренебречь по сравнению со всеми указанными выше длинами.
 Подробнее
Подробнее
Лифтер высотного здания, будучи человеком пунктуальным, повесил на стену лифта точные маятниковые часы, чтобы знать, когда кончается рабочий день. Время движения лифта с ускорением, направленным вверх и направленным вниз, одинаково (по неподвижным часам); одинаковы также модули ускорений.
Как вы думаете, закончит ли лифтер работу вовремя, переработает или недоработает?
Подробнее
Зависимость координаты материальной точки от времени дастся законом: $x(t) = A \cos \omega t + B \sin \omega t$. Чему равна амплитуда колебаний?
Подробнее
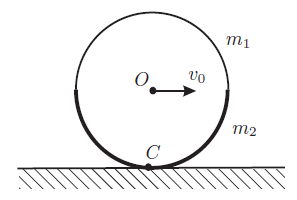
На горизонтальной шероховатой поверхности находится обруч радиуса $R$, склеенный из двух однородных половинок массами $m_{1}$ и $m_{2}$ (рис. ).
1. При какой минимальной скорости $v_{0}$ центра $O$ обруч совершит полный оборот без проскальзывания?
2. Определите период малых колебаний обруча вблизи положения равновесия.
3. Найдите максимально возможный угол $\alpha_{max}$ наклона опорной плоскости к горизонту, при котором обруч, находящееся на ней, ещё остаётся в равновесии.
 Подробнее
Подробнее