Задача по физике - 577
2014-06-01 
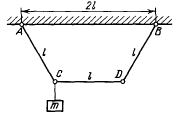
Три невесомых шарнирно связанных в точках С и D стержня длины $l$ каждый закреплены также шарнирно в точках А и В, лежащих на одной горизонтали (рис.); длина $AB = 2l$. К шарниру С подвесили груз массой $m$.
Определите минимальную силу $F_{min}$, приложенную к шарниру D, при которой средний стержень сохраняет горизонтальное положение.
Решение:

Поскольку шарнир С находится в равновесии, сумма сил, действующих на него, равна нулю. Записывая силы, действующие на шарнир С, в проекции на ось, перпендикулярную АС, получим
$(m+m_{ш}) g \sin \alpha = T \cos \alpha$, (1)
где $m_{ш}$- - масса шарнира. Аналогично, из условия равновесия шарнира D и условия горизонтальности среднего стержня следует, что
$T \cos \alpha = F \cos \beta + m_{ш}g \sin \alpha$. (2)
Из (1) и (2) получаем
$F =\frac{T \cos \alpha – m_{ш} g \sin \alpha}{\cos \beta} = \frac{mg \sin \alpha}{ \cos \beta} \geq mg \sin \alpha$
Таким образом, минимальная сила $F_{min}$, при которой средний стержень сохраняет горизонтальное положение, равна
$F_{min}=mg \sin \alpha = mg/2$
и направлена перпендикулярно стержню ВD.
Три невесомых шарнирно связанных в точках С и D стержня длины $l$ каждый закреплены также шарнирно в точках А и В, лежащих на одной горизонтали (рис.); длина $AB = 2l$. К шарниру С подвесили груз массой $m$.
Определите минимальную силу $F_{min}$, приложенную к шарниру D, при которой средний стержень сохраняет горизонтальное положение.

Решение:

Поскольку шарнир С находится в равновесии, сумма сил, действующих на него, равна нулю. Записывая силы, действующие на шарнир С, в проекции на ось, перпендикулярную АС, получим
$(m+m_{ш}) g \sin \alpha = T \cos \alpha$, (1)
где $m_{ш}$- - масса шарнира. Аналогично, из условия равновесия шарнира D и условия горизонтальности среднего стержня следует, что
$T \cos \alpha = F \cos \beta + m_{ш}g \sin \alpha$. (2)
Из (1) и (2) получаем
$F =\frac{T \cos \alpha – m_{ш} g \sin \alpha}{\cos \beta} = \frac{mg \sin \alpha}{ \cos \beta} \geq mg \sin \alpha$
Таким образом, минимальная сила $F_{min}$, при которой средний стержень сохраняет горизонтальное положение, равна
$F_{min}=mg \sin \alpha = mg/2$
и направлена перпендикулярно стержню ВD.





