Задача по физике - 136
2014-05-31 
Тонкая проволочная горизонтально расположенная рамка, имеющая форму окружности длиной $l = 10 см $, стянута мыльной пленкой. Коэффициент поверхностного натяжения $\sigma = 10^{-2} Н/м$. Найдите наибольшую возможную массу пленки.
Решение:
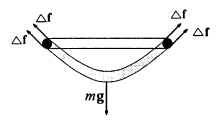
На рис. показано вертикальное поперечное сечение, проведенное через середину проволочного кольца. На мыльную пленку в этом сечении действуют: сила тяжести $m \bar{g}$, направлена вниз, и силы $\Delta \bar{f}$ поверхностного натяжения, направленные по касательной к поверхности пленки в точках контакта пленки с кольцом. Направления этих сил составляют некоторый угол $\alpha$ с вертикалью.
Рассматривая точки поверхности пленки, расположенные на противоположных концах диаметра кольца, нетрудно сообразить, что горизонтальные составляющие сил $\Delta \bar{f}$ в этих точках направлены в противоположные стороны и уравновешивают друг друга. Поэтому равнодействующая $\bar{F}$ всех сил $\Delta \bar{f}$, приложенных к пленке со стороны кольца, будет направлена вверх; она складывается из вертикальных составляющих всех сил $\Delta \bar{f}$. Учитывая, что пленка имеет две поверхности, получаем
$F= 2 \sigma l \cos \alpha$
Так как пленка покоится, то проекция на вертикальное направление суммы всех приложенных к ней сил равна нулю, т. е.
$F – mg = 2 \sigma l \cos \alpha – mg = 0$.
Отсюда находим
$m = 2 \sigma l \cos \alpha /g$. (1)
В условиях равновесия масса пленки достигает своего максимального значения $m_{max}$ при $\alpha = 0$, когда все силы поверхностного натяжения $\Delta \bar{f}$ направлены вертикально вверх. Полагая в (1) $\alpha = 0$, получаем
$m_{max}=2 \sigma l / g = 0,2 г$.
Если $ m > m_{max}$, то пленка отрывается от кольца.
Тонкая проволочная горизонтально расположенная рамка, имеющая форму окружности длиной $l = 10 см $, стянута мыльной пленкой. Коэффициент поверхностного натяжения $\sigma = 10^{-2} Н/м$. Найдите наибольшую возможную массу пленки.

Решение:
На рис. показано вертикальное поперечное сечение, проведенное через середину проволочного кольца. На мыльную пленку в этом сечении действуют: сила тяжести $m \bar{g}$, направлена вниз, и силы $\Delta \bar{f}$ поверхностного натяжения, направленные по касательной к поверхности пленки в точках контакта пленки с кольцом. Направления этих сил составляют некоторый угол $\alpha$ с вертикалью.
Рассматривая точки поверхности пленки, расположенные на противоположных концах диаметра кольца, нетрудно сообразить, что горизонтальные составляющие сил $\Delta \bar{f}$ в этих точках направлены в противоположные стороны и уравновешивают друг друга. Поэтому равнодействующая $\bar{F}$ всех сил $\Delta \bar{f}$, приложенных к пленке со стороны кольца, будет направлена вверх; она складывается из вертикальных составляющих всех сил $\Delta \bar{f}$. Учитывая, что пленка имеет две поверхности, получаем
$F= 2 \sigma l \cos \alpha$
Так как пленка покоится, то проекция на вертикальное направление суммы всех приложенных к ней сил равна нулю, т. е.
$F – mg = 2 \sigma l \cos \alpha – mg = 0$.
Отсюда находим
$m = 2 \sigma l \cos \alpha /g$. (1)
В условиях равновесия масса пленки достигает своего максимального значения $m_{max}$ при $\alpha = 0$, когда все силы поверхностного натяжения $\Delta \bar{f}$ направлены вертикально вверх. Полагая в (1) $\alpha = 0$, получаем
$m_{max}=2 \sigma l / g = 0,2 г$.
Если $ m > m_{max}$, то пленка отрывается от кольца.





