Задача по физике - 132
2014-05-31 
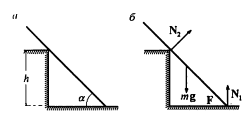
Однородный стержень длиной $l$ опирается о пол и ступеньку (рис, а). Коэффициент трения между стержнем и полом $\mu =1$, трения между стержнем и ступенькой нет. При какой высоте ступеньки стержень может находиться в равновесии, если угол $ \alpha = 45^{\circ}$.
Решение:
На стержень действуют силы (рис. б): тяжести $m \bar{g}$, реакции пола $\bar{N_{1}}$, реакции ступеньки $\bar{N_{2}}$, трения $F_{т}$, направленная горизонтально. Если стержень покоится, то сумма действующих на него сил равна нулю:
$m \bar{g} + \bar{N_{1}} + \bar{N_{2}}+F_{т} = 0$.
Проецируя это векторное равенство на горизонтальное и вертикальные направления, получаем
$F_{т} – N_{2} \sin \alpha = 0$, (1)
$-mg + N_{1}+N_{2} \cos \alpha = 0$. (2)
С учетом того, что $ \alpha = 45^{\circ}$ и, следовательно, $\sin \alpha = \cos \alpha = \frac{\sqrt{2}}{2}$
равенства (1) и (2) принимают вид
$F_{т}=\frac{1}{\sqrt{2}} N_{2}, mg = N_{1} - \frac{1}{\sqrt{2}} N_{2}$.
Когда стержень находится в равновесии, должна быть равна нулю и сумма моментов этих сил относительно произвольно выбранной точки. Рассматривая моменты относительно левого конца стержня получаем
$\frac{mgl}{2 \sqrt{2}} - \sqrt{2} h N_{2} = 0$.
Отсюда
$N_{2}= \frac{mgl}{4h}$.
Из системы уравнении (1) - (3) находим
$F_{т}=\frac{mgl}{4 \sqrt{2} h}, N_{1} = mg \left ( 1- \frac{l}{4 \sqrt{2} h} \right )$.
Учитывая, что при равновесии сила сухого трения $F_{т} \leq \mu N_{1} = N_{1}$
(так как $\mu = 1$), получаем условие равновесия стержня в виде
$\frac{mgl}{4 \sqrt{2} h} \leq mg \left ( 1 - \frac{l}{4 \sqrt{2} h} \right )$.
Этому неравенству эквивалентно следующее:
$h \geq \frac{l}{2 \sqrt{2}}$.
С другой стороны, в положении равновесия всегда
$h \leq l \sin \alpha = l / \sqrt{2}$.
Итак, равновесие стержня возможно, если высота ступеньки такова, что выполняются неравенства
$\frac{l}{2 \sqrt{2}} \leq h \leq \frac{l}{\sqrt{2}}$.
Однородный стержень длиной $l$ опирается о пол и ступеньку (рис, а). Коэффициент трения между стержнем и полом $\mu =1$, трения между стержнем и ступенькой нет. При какой высоте ступеньки стержень может находиться в равновесии, если угол $ \alpha = 45^{\circ}$.

Решение:
На стержень действуют силы (рис. б): тяжести $m \bar{g}$, реакции пола $\bar{N_{1}}$, реакции ступеньки $\bar{N_{2}}$, трения $F_{т}$, направленная горизонтально. Если стержень покоится, то сумма действующих на него сил равна нулю:
$m \bar{g} + \bar{N_{1}} + \bar{N_{2}}+F_{т} = 0$.
Проецируя это векторное равенство на горизонтальное и вертикальные направления, получаем
$F_{т} – N_{2} \sin \alpha = 0$, (1)
$-mg + N_{1}+N_{2} \cos \alpha = 0$. (2)
С учетом того, что $ \alpha = 45^{\circ}$ и, следовательно, $\sin \alpha = \cos \alpha = \frac{\sqrt{2}}{2}$
равенства (1) и (2) принимают вид
$F_{т}=\frac{1}{\sqrt{2}} N_{2}, mg = N_{1} - \frac{1}{\sqrt{2}} N_{2}$.
Когда стержень находится в равновесии, должна быть равна нулю и сумма моментов этих сил относительно произвольно выбранной точки. Рассматривая моменты относительно левого конца стержня получаем
$\frac{mgl}{2 \sqrt{2}} - \sqrt{2} h N_{2} = 0$.
Отсюда
$N_{2}= \frac{mgl}{4h}$.
Из системы уравнении (1) - (3) находим
$F_{т}=\frac{mgl}{4 \sqrt{2} h}, N_{1} = mg \left ( 1- \frac{l}{4 \sqrt{2} h} \right )$.
Учитывая, что при равновесии сила сухого трения $F_{т} \leq \mu N_{1} = N_{1}$
(так как $\mu = 1$), получаем условие равновесия стержня в виде
$\frac{mgl}{4 \sqrt{2} h} \leq mg \left ( 1 - \frac{l}{4 \sqrt{2} h} \right )$.
Этому неравенству эквивалентно следующее:
$h \geq \frac{l}{2 \sqrt{2}}$.
С другой стороны, в положении равновесия всегда
$h \leq l \sin \alpha = l / \sqrt{2}$.
Итак, равновесие стержня возможно, если высота ступеньки такова, что выполняются неравенства
$\frac{l}{2 \sqrt{2}} \leq h \leq \frac{l}{\sqrt{2}}$.





