Задача по физике - 131
2014-05-31 
Кубический ящик стоит на полу. При каких значениях коэффициента трения между ящиком и полом легче двигать ящик, а не кантовать?
Решение:
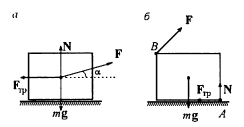
Найдем сначала минимальную силу $\bar {F_{I}}$, которую надо приложить, чтобы сдвинуть ящик, при условии, что эта сила действует под некоторым углом $\alpha$ к горизонту. Все силы, действующие при этом на ящик, показаны на (рис. а). Помимо силы $\bar{F}$ действуют силы тяжести $m \bar{g}$, нормальной реакции пола $\bar{N}$, трения $\bar{F_{т}}$. При $\bar{F} = \bar{F_{I}}$ ящик начинает двигаться вправо с нулевым ускорением, при этом
$F_{т}=\mu N$, (1)
а сумма всех приложенных к ящику сил равна нулю:
$\bar{F_{I}+\bar{N}+m \bar{g}+\bar{F_{т}}}=0$, (2)
или в проекциях на горизонтальное и вертикальное направления:
$F_{I}\cos \alpha – F_{т} = 0$, (3)
$F_{I} \sin \alpha + N - mg = 0$. (4)
Из уравнений (1) - (4) находим
$F_{I}= mg \frac{\mu}{\cos \alpha + \mu \sin \alpha}$. (5)
Сила $F_{I}$ принимает минимальное значение $F_{Imin}$ при таком угле $\alpha$, при котором знаменатель правой части равенства (5) максимален.
Преобразуем выражение в знаменателе. С этой целью введем угол $\theta$, для которого
$\sin \theta = \frac{\mu}{\sqrt{1+\mu^{2}}}$, (6)
$\cos \theta = \frac{1}{\sqrt{1+\mu^{2}}}$. (7)
Это можно сделать, так как правые части выражений (6) и (7) всегда меньше единицы и соотношение $\sin^{2} \theta + \cos^{2} \theta = 1$ выполняется.
Очевидно, что
$\cos \alpha + \mu \sin \alpha = \sqrt{1+\mu^{2}}(\cos \alpha \cos \theta + \sin \alpha sin \theta) = \sqrt{1+\mu^{2}} \cos (\alpha - \theta)$
Это выражение достигает максимального значения $\sqrt{1+\mu^{2}}$ при $\alpha= \theta$. Таким образом, из (5) находим
$F_{Imin} = mg \frac{\mu}{\sqrt{1+\mu^{2}}}$. (8)
Ящик начинает переворачиваться под действием силы $\bar{F}$, если она достигает некоторого значения $F_{II}$. Чтобы перекантовать ящик с помощью силы $F_{II}$, нужно, чтобы создаваемый ею относительно точки А момент $F_{II}L$ был равен моменту $mga/2$, создаваемому силой тяжести (рис. б):
$F_{II}L=mg \frac {a}{2}$, (9)
где $a$ - длина ребра ящика; $L$ - плечо силы $F$. Из соотношения (9) находим
$F_{II}=mg \frac{a}{2L}$.
Сила $F_{II}$ достигает своего наименьшего значения $F_{IImin}$ при максимальной длине плеча $L$, равной диагонали АВ ящика: $L = \sqrt{2} a$
Таким образом,
$F_{IImin}=\frac{mg}{2 \sqrt{2}}$. (10)
Ящик выгоднее двигать, если
$F_{Imin} < F_{IImin}$.
Подставляя в это неравенство выражения для $F_{Imin}$ и $F_{IImin}$ из (8) и (10), получаем
$\frac{\mu}{\sqrt{1+\mu^{2}}} < \frac{1}{2 \sqrt{2}}$.
Отсюда $\mu < 1/\sqrt{7}$. При таких значениях коэффициента трения легче двигать ящик, а при $\mu > 1/\sqrt{7}$ легче кантовать.
Однако надо еще проверить, при каких значениях коэффициента трения ящик будет переворачиваться.
Чтобы ящик переворачивался, а не скользил, надо, чтобы сумма сил, действующих на ящик, заведомо равнялась нулю,- условие которое в нашем случае можно переписать в проекциях на горизонтальное и вертикальное направления как
$\frac{F}{\sqrt{2}}- F_{т} = 0$, (11)
$\frac{F}{\sqrt{2}}+N-mg=0$. (12)
Скольжение отсутствует при выполнении неравенства
$F_{т} < \mu N$, (13)
Из (11) - (13) получаем неравенство $\mu > 1/3$, которое согласуется с полученным выше результатом, так как $1/3 < 1/\sqrt{7}$.
Кубический ящик стоит на полу. При каких значениях коэффициента трения между ящиком и полом легче двигать ящик, а не кантовать?

Решение:
Найдем сначала минимальную силу $\bar {F_{I}}$, которую надо приложить, чтобы сдвинуть ящик, при условии, что эта сила действует под некоторым углом $\alpha$ к горизонту. Все силы, действующие при этом на ящик, показаны на (рис. а). Помимо силы $\bar{F}$ действуют силы тяжести $m \bar{g}$, нормальной реакции пола $\bar{N}$, трения $\bar{F_{т}}$. При $\bar{F} = \bar{F_{I}}$ ящик начинает двигаться вправо с нулевым ускорением, при этом
$F_{т}=\mu N$, (1)
а сумма всех приложенных к ящику сил равна нулю:
$\bar{F_{I}+\bar{N}+m \bar{g}+\bar{F_{т}}}=0$, (2)
или в проекциях на горизонтальное и вертикальное направления:
$F_{I}\cos \alpha – F_{т} = 0$, (3)
$F_{I} \sin \alpha + N - mg = 0$. (4)
Из уравнений (1) - (4) находим
$F_{I}= mg \frac{\mu}{\cos \alpha + \mu \sin \alpha}$. (5)
Сила $F_{I}$ принимает минимальное значение $F_{Imin}$ при таком угле $\alpha$, при котором знаменатель правой части равенства (5) максимален.
Преобразуем выражение в знаменателе. С этой целью введем угол $\theta$, для которого
$\sin \theta = \frac{\mu}{\sqrt{1+\mu^{2}}}$, (6)
$\cos \theta = \frac{1}{\sqrt{1+\mu^{2}}}$. (7)
Это можно сделать, так как правые части выражений (6) и (7) всегда меньше единицы и соотношение $\sin^{2} \theta + \cos^{2} \theta = 1$ выполняется.
Очевидно, что
$\cos \alpha + \mu \sin \alpha = \sqrt{1+\mu^{2}}(\cos \alpha \cos \theta + \sin \alpha sin \theta) = \sqrt{1+\mu^{2}} \cos (\alpha - \theta)$
Это выражение достигает максимального значения $\sqrt{1+\mu^{2}}$ при $\alpha= \theta$. Таким образом, из (5) находим
$F_{Imin} = mg \frac{\mu}{\sqrt{1+\mu^{2}}}$. (8)
Ящик начинает переворачиваться под действием силы $\bar{F}$, если она достигает некоторого значения $F_{II}$. Чтобы перекантовать ящик с помощью силы $F_{II}$, нужно, чтобы создаваемый ею относительно точки А момент $F_{II}L$ был равен моменту $mga/2$, создаваемому силой тяжести (рис. б):
$F_{II}L=mg \frac {a}{2}$, (9)
где $a$ - длина ребра ящика; $L$ - плечо силы $F$. Из соотношения (9) находим
$F_{II}=mg \frac{a}{2L}$.
Сила $F_{II}$ достигает своего наименьшего значения $F_{IImin}$ при максимальной длине плеча $L$, равной диагонали АВ ящика: $L = \sqrt{2} a$
Таким образом,
$F_{IImin}=\frac{mg}{2 \sqrt{2}}$. (10)
Ящик выгоднее двигать, если
$F_{Imin} < F_{IImin}$.
Подставляя в это неравенство выражения для $F_{Imin}$ и $F_{IImin}$ из (8) и (10), получаем
$\frac{\mu}{\sqrt{1+\mu^{2}}} < \frac{1}{2 \sqrt{2}}$.
Отсюда $\mu < 1/\sqrt{7}$. При таких значениях коэффициента трения легче двигать ящик, а при $\mu > 1/\sqrt{7}$ легче кантовать.
Однако надо еще проверить, при каких значениях коэффициента трения ящик будет переворачиваться.
Чтобы ящик переворачивался, а не скользил, надо, чтобы сумма сил, действующих на ящик, заведомо равнялась нулю,- условие которое в нашем случае можно переписать в проекциях на горизонтальное и вертикальное направления как
$\frac{F}{\sqrt{2}}- F_{т} = 0$, (11)
$\frac{F}{\sqrt{2}}+N-mg=0$. (12)
Скольжение отсутствует при выполнении неравенства
$F_{т} < \mu N$, (13)
Из (11) - (13) получаем неравенство $\mu > 1/3$, которое согласуется с полученным выше результатом, так как $1/3 < 1/\sqrt{7}$.





