Задача по физике - 130
2014-05-31 
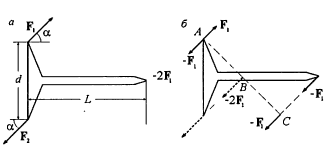
Для ориентации космического корабля включают два двигатели, развивающие силу тяги $\bar{F_{1}}$ и $\bar{F_{2}} = - 2 \bar{F_{1}}$. Можно ли заменить эти два двигателя одним так, чтобы он оказывал такое же воздействие на движение корабля? Если можно, то куда его надо поместить и какую силу тяги он должен развивать? Расположение двигателей, направление сил тяги и размеры корабля указаны на (рис. а). Положение центра тяжести корабля неизвестно, $\alpha = 45^{\circ}, L = 3d/2$
Решение:
Найдем равнодействующую двух антипараллельных сил $\bar{F_{1}}$ и $\bar{F_{2}}$, не равных друг другу по величине. Расстояние между направлениями действия этих сил равно $l = d/\sqrt{2}$.
Разложим силу $\bar {F_{2}} = - 2 \bar {F_{1}}$, приложенную в точке В (рис. б), на две силы - силу $\bar {F_{A}} = - \bar {F_{1}}$, приложенную в точке A, и силу
$\bar {F_{C}} = - \bar {F_{1}}$, приложенную в точке С {АВ = ВС). Силы в точке А
компенсируют друг друга. Следовательно, суммарная сила равная $- \bar {F_{1}}$ и приложена к произвольной точке, принадлежащей линии, проходящей через точку С. Исходя из геометрии корабля, нетрудно показать, что эта линия проходит через "нос" корабля.
Для ориентации космического корабля включают два двигатели, развивающие силу тяги $\bar{F_{1}}$ и $\bar{F_{2}} = - 2 \bar{F_{1}}$. Можно ли заменить эти два двигателя одним так, чтобы он оказывал такое же воздействие на движение корабля? Если можно, то куда его надо поместить и какую силу тяги он должен развивать? Расположение двигателей, направление сил тяги и размеры корабля указаны на (рис. а). Положение центра тяжести корабля неизвестно, $\alpha = 45^{\circ}, L = 3d/2$

Решение:
Найдем равнодействующую двух антипараллельных сил $\bar{F_{1}}$ и $\bar{F_{2}}$, не равных друг другу по величине. Расстояние между направлениями действия этих сил равно $l = d/\sqrt{2}$.
Разложим силу $\bar {F_{2}} = - 2 \bar {F_{1}}$, приложенную в точке В (рис. б), на две силы - силу $\bar {F_{A}} = - \bar {F_{1}}$, приложенную в точке A, и силу
$\bar {F_{C}} = - \bar {F_{1}}$, приложенную в точке С {АВ = ВС). Силы в точке А
компенсируют друг друга. Следовательно, суммарная сила равная $- \bar {F_{1}}$ и приложена к произвольной точке, принадлежащей линии, проходящей через точку С. Исходя из геометрии корабля, нетрудно показать, что эта линия проходит через "нос" корабля.





